Salut,
Je déterre un peu ce post parce que j'ai pas mal de nouveau à ce sujet.
J'avais dis sur quelques post que je faisais un projet pour mes études en rapport avec les roues sans moyeu dans le vélo. Je devrais présenter ce projet-étude en fin d'année à l'oral. Je vous présente donc mes avancées parce que certain me l'on demandé sur ce forum et pour avoir aussi vos remarques et questions, ça peux me permettre d'améliorer tout ça.
Roue sans moyeu
L'idée de la roue sans moyeu ne vient pas de moi, c'est un système breveté mais les seuls prototypes existants sont des motos principalement. L'avantage indéniable c'est que c'est beau et le but de mon étude et de voir si cette configuration apporte aussi quelque chose d'un point de vue mécanique.
Prototype virtuel
La première étape fut de créer un proto sur un logiciel de CAO. Le bmx que montre le lien du premier post de ce sujet utilise des roulements de la taille de la roue. La cage intérieure du roulement est liée au cadre, la cage extérieure au pneu. L'inconvénient c'est que l'on a des masses importante (un roulement aussi gros pèse lourd) loin du centre de rotation, ce qui donne de grandes forces gyroscopique. Et sur un vélo on ressent beaucoup ces forces. C'est pour ça qu'on dit souvent qu'il faut mieux commencer par réduire le poids des roues quand on veut réduire le poids d'un vélo.
J'ai donc chercher une solution différente de celle-là. J'ai eu l'idée d'adapter une roue de vélo normale, ce qui me permettra en plus de réaliser facilement un proto réel. Je suis arrivé à quelque chose qui ressemble à ça :

J'ai modélisé une jante que j'avais d'un vieux bike, la chambre à aire le pneu avec le plus de détails possibles pour respecter au mieux les volumes et les masses.
Étude cinématique-inertie
La modélisation de cette roue sans moyeu m'a permis d'obtenir la matrice d'inertie de la dite roue. En gros c'est un ensemble de 3 vecteurs à 3 coordonnées chacun qui permet de savoir comment sont réparties les masses dans les volume, pour simplifier les choses.
J'ai aussi modéliser une roue classique avec moyeu en 36 rayons croisés par 3 pour pouvoir comparer les résultats obtenus. J'ai obtenu les deux matrices d'inerties suivante :
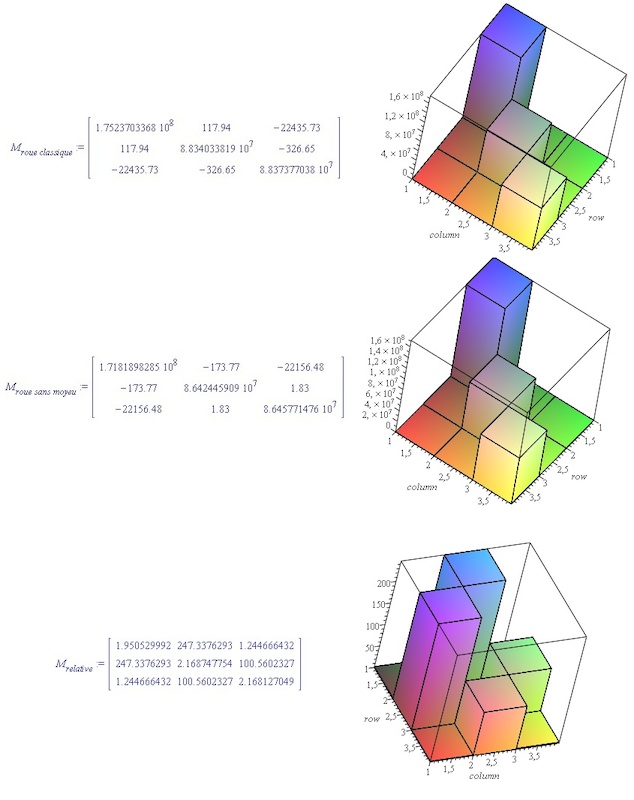
La première matrice est celle de la roue classique, la deuxième celle de la roue sans moyeu, la troisième est une matrice relative en pourcentage obtenue à partir des deux premières. En gros de combien est ce que la première matrice est plus ou moins grande que la deuxième

.
Les histogrammes sont les tracés des hauteurs de chacune des coordonnées de la matrice correspondante. On voit que les diagonales sont beaucoup plus importantes que les autres coordonnées. Ca ça veut dire que notre roue est plutôt équilibrée. Sur les roues des voitures ont rajoute des masselotte pour équilibrer les roues afin d'être sur qu'elles ne vibrent pas lorsque l'on roule à haute vitesse. Cette équilibrage revient à changer la répartition des masses par rapport au volume pour annuler les termes non diagonaux de ces matrices d'inertie. Donc nos roues de vélo ne sont pas tout à fait équilibrées...
La deuxième chose à noter c'est que la matrice relative (la troisième) montre que les différences entre nos deux premières matrices se trouvent sur les termes non diagonaux.
Ces matrices servent à calculer les forces que va exercer la roue une fois qu'elle sera en rotation.
J'ai donc cherché un exemple de calcul où seuls les termes non diagonaux intervenais, (c'est à dire le cas où les roues sont les plus « différentes » ). Ce cas correspondant à une vitesse de rotation de la roue constante et un angle de fourche constant. J'ai tracé ces forces pour plusieurs valeurs de vitesse de rotation et d'angle de fourche.
J'arrive à ces résultats là :
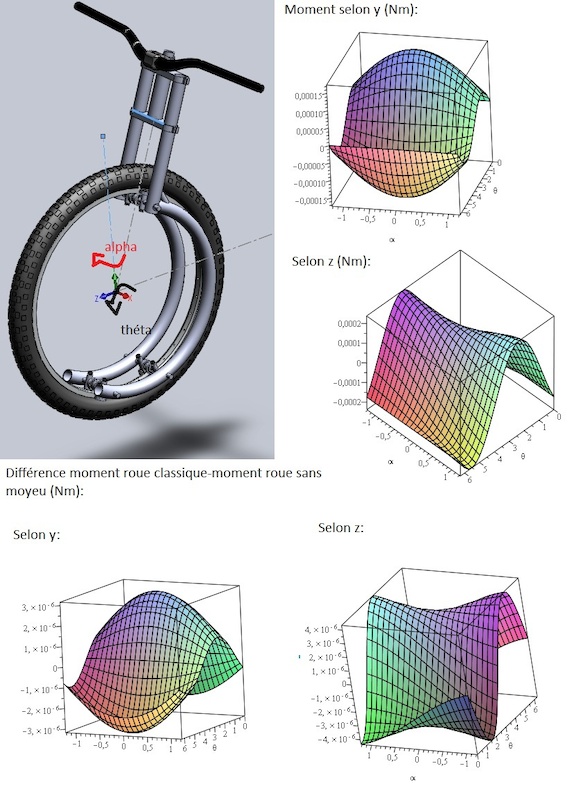
On voit que les valeurs maximales sont de l'ordre de 4,10^(-6) Nm. Pour vous donner une idée : Si on met une masse de 1kg au bout d'une barre d'un mètre de long et que l'on tient cette barre on aura une force (qu'on appelle alors un moment) de 1Nm dans la main. Donc les moments obtenus ici sont vraiment minuscules.
Deux conclusions :
1) c'est normal qu'on n'équilibre pas nos roues de vélos au vu du moment minuscule que génère le « déséquilibrage »
2) Notre roue sans moyeu n'apporte rien d'un point de vue inertiel...
Rigidité
En matière de rigidité par contre les différences entre roue avec et sans moyeu risquent d'être bien plus importantes. Si on met des rayon sur nos roues c'est d'abord pour les rigidifier. Là pour quantifier les choses c'est plus compliqué. J'ai donc fait l'expérience suivante sur mon logiciel de 3D :

On coince la jante entre deux éprouveuses on fixe celle du bas et on applique une force sur celle du haut.
Après expérience on arrive à ce genre de tracé :
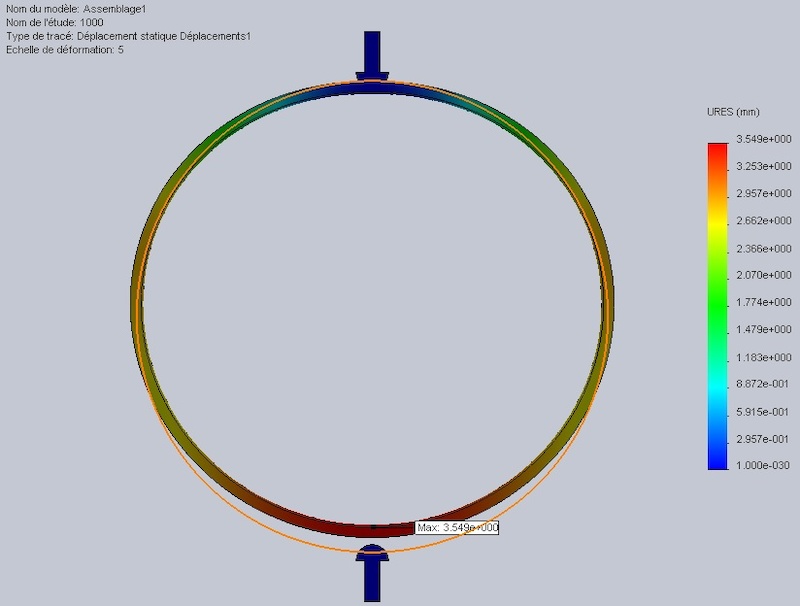
Ici avec une échelle x5 et une force de 1000N soit 100kg posés sur l'éprouveuse du haut.
J'ai fait l'expérience pour plusieurs valeurs de la force et j'arrive à la droite suivante qui représente le déplacement max en fonction de la force appliquée : (pour la roue sans moyeu)
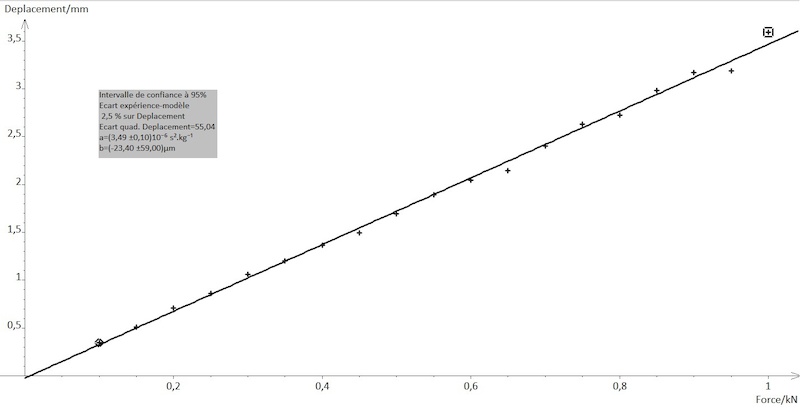
Pour pouvoir comparer il faut que je fasse la même chose sur la roue avec moyeu. Le soucis étant que les rayons appliquent une force sur la jante et qu'il me faut connaître cette force pour pouvoir faire l'expérience.
J'avais créé un autre sujet sur 26in pour ce soucis là. La force qu'applique un rayon sur la jante est la même que celle qu'il applique sur le moyeu et cette force résulte du faite que le rayon soit tendu.
Pour déterminer la tension d'un rayon on utilise un tensiomètre :
http://zorglub1422.free.fr/images/velo/entretien/roue/IMG_1414.JPG
On vient coincer un rayon entre 3 galets, 2 fixés et un mobile. On déplace le mobile qui vient tordre le rayon et le déplacement de ce galet dépend de la tension du rayon. Le fabricant de ce tensiomètre donne des tables liant la valeur du déplacement à la force qu'exerce le tensiomètre.
Sur mon logiciel j'ai donc modélisé un rayon de 2mm de diamètre dont j'ai fixé les deux extrémités.
J'applique la force que me donne la table du tensiomètre J'arrive à ça :
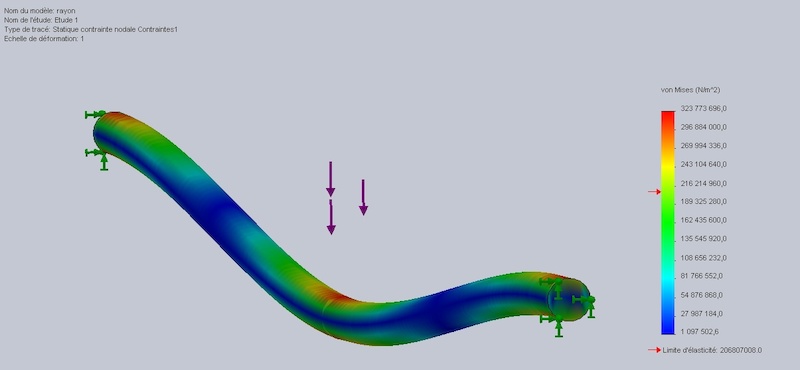
C'est un tracé de contrainte. En gros je sais qu'elle force subit chaque mm^2 des extrémités de mon rayon, en multipliant cette contrainte par la surface j'obtiens la force qu'exerce mon rayon sur ma jante. En gros quelque chose de l'ordre de 400N. C'est une force importante mais vu qu'elle est répartie tout autour de la roue elle ne la déforme pas.
Ensuite je regarde un calculateur de longueur de rayon pour une roue standard j'arrive à ça :
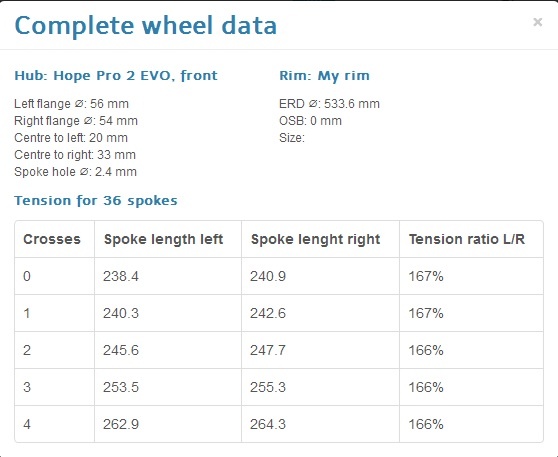
Ce calculateur me donne aussi le rapport entre la tension sur la nappe de rayon de gauche et celle de la nappe de droite. Ces tensions sont différentes parce que la jante n'est pas centrée sur le moyeu mais sur la fourche. Pour déplacer le cerclage vers la droite on tend plus la nappe de droite par exemple.
Je peux maintenant faire ma simulation sur la roue avec moyeu. Je met ma force de 400N sur une des nappes et de 239 sur l'autre (400/239=1,67

). La direction de la force étant l'axe du rayon.
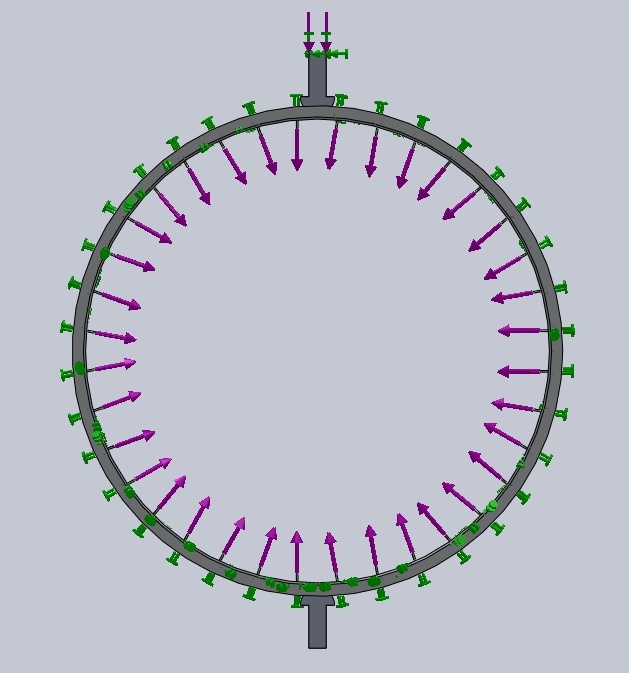
Voilà où j'en suis aujourd'hui je fait ma série d'expérience avec la roue avec moyeu. Les premiers résultats montrent que la différence n'est pas super importante.
Une dernière expérience sera d'essayer d'appliqué un couple à l'éprouveuse et pas une force. En gros mettre une force qui la ferait tourner sur elle même et là je pense que la différence sera vraiment importante.
Je vais ensuite modifier mon modèle 3D de la roue sans moyeu et rajouter de la matière dans l'idée de récupérer de la rigidité. Or je vais rajouter du métal, donc de la masse loin du centre de la roue et là la matrice d'inertie va devenir dégueulasse...
En conclusion, on est pas près de lâcher nos bonnes vieilles roues à rayon. Enlever les rayons et le moyeu n'améliore pas les forces inertielles mais réduit la rigidité. Le rayon est donc un super compromis.
J'ai aussi dans l'idée de faire un proto réel de cette roue pour voir ce que ça donne en vrai. J'ai commandé les roulements j'ai déjà les tubes je vous mettrai des photos

.
Voilà si des courageux arrivent à tout lire je serai très heureux d'avoir vos avis vos réactions. Merci !














inscrit le 9/9/09
20 messages